샤모스-호이 알고리즘 (Shamos-Hoey Algorithm)

서론

다음과 같은 문제를 생각해봅시다.

 

"좌표평면에 $N$개의 선분이 있고, 이들 중 서로 교차하는 선분 쌍이 존재하는지 판별하라."

 

이 문제를 푸는 가장 간단한 방법은 모든 선분 쌍에 대해 서로 교차하는지 판별하는 것입니다. 선분 쌍은 $O(N^2)$개이고, 두 선분이 교차하는지는 $O(1)$에 판정할 수 있기 때문에 시간복잡도는 $O(N^2)$이 됩니다.

 

이 글에서는 위 문제를 $O(N\log{N})$에 풀 수 있는 샤모스-호이 알고리즘에 대해 설명하겠습니다.

 

가정

알고리즘을 소개하기에 앞서, 몇 가지 가정을 하도록 하겠습니다.

 

1. $y$축에 평행한 선분이 존재하지 않는다.

2. 한 선분의 끝 점이 다른 선분이나 끝 점 위에 있는 것도 교차하는 것이다.

3. 세 선분이 한 점에서 교차하는 경우는 존재하지 않는다.

 

위 가정이 성립하지 않는 경우에 대해서는 뒤에서 설명하겠습니다.

 

아이디어

샤모스-호이 알고리즘은 스위핑 알고리즘을 기반으로 작동합니다. $y$축에 평행한 직선이 -INF부터 INF까지 움직이면서 선분에 대한 정보를 관리하는 방식을 이용합니다.

 

현재 sweep line이 $x = t$라고 해봅시다. 두 선분 $a$, $b$에 대해 $a$와 $b$가 모두 sweep line과 교차한다면, $a$와 $b$는 "$t$에서 비교 가능"하다고 정의하겠습니다. 이때, $a$와 $b$가 sweep line과 교차하는 점을 각각 $P$, $Q$라고 하고, $P$의 $y$좌표가 $Q$보다 크다면, "$t$에서 $a$가 $b$보다 크다"라고 정의하겠습니다. 이를 $a \succcurlyeq_{t} b$라고 표기하도록 하겠습니다.

 

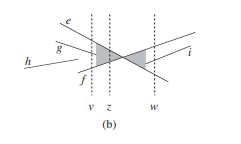
CLRS 1023p Figure 33.4 (b)

이해를 돕기 위해 위 그림을 보면 $e$와 $f$는 $v$, $z$, $w$에서 모두 비교가 가능하지만, $e$와 $g$는 $z$에서 비교 불가능합니다. 또한, $e \succcurlyeq_{z} f$와 $e \succcurlyeq_{w} f$가 성립합니다.

 

여기서 한 가지 중요한 성질을 관찰할 수 있습니다.

 

성질: 어떤 두 선분 $a$와 $b$가 $x = t_{0}$에서 교차한다면, $t_{0}$를 기준으로 크기 관계가 뒤바뀌고, 교차하지 않는다면 비교 가능한 모든 sweep line에 대해 크기 관계가 모두 동일하다.

 

위 그림에서는 $e$와 $g$의 크기 관계는 항상 $e \succcurlyeq g$가 성립하지만, $e$와 $f$에 대해서는 교점을 기준으로 크기 관계가 뒤바뀜을 확인할 수 있습니다.

 

샤모스-호이 알고리즘은 이 성질을 기반으로 작동합니다.

 

작동 과정

sweep line을 실제로 -INF부터 INF까지 움직이면서 작동하는 건 불가능하기 때문에, 선분의 양 끝점에 대해서만 sweep line을 움직일 것입니다.

 

더 엄밀히 말하자면, event point라는 것은 다음과 같이 정의됩니다.

 

event point $(x, e, y, s)$는 $(x, y)$가 $s$번 선분의 끝 점 중 하나이고, $x$좌표가 더 작은 끝 점일 경우 $e = 0$, 그렇지 않을 경우 $e = 1$이다.

 

샤모스 호이 알고리즘은 이 event point들의 집합 $E$를 사전 순 정렬한 후, sweep line을 움직이면서 작동합니다.

CLRS 1025p

위 의사코드가 샤모스-호이 알고리즘의 의사코드입니다. 이를 한 줄씩 분석해봅시다.

 

일단, 1번 줄에서 집합 $T$를 잡습니다. 이는 정렬성을 유지하는 집합으로, c++에서 std::set과 동일합니다. 집합 T의 원소는 선분이고, 비교조건은 현재 sweep line의 $x$좌표인 $t$에서의 비교조건입니다. (교점이 존재하면 크기 관계가 뒤바뀔 수 있는데 이에 대한 자세한 설명은 뒷부분에서 하겠습니다.)

 

2번 줄에서는 선분의 끝점들을 특정 기준에 따라 정렬합니다. 이는 event point들을 사전 순 정렬하는 것과 동일한 정렬입니다.

 

3~11번 줄은 sweep line을 움직이며, event point들을 처리하는 과정입니다.

 

4~7번 줄은 현재 event point가 선분의 왼쪽 끝점일 경우, 즉 $e = 0$인 경우입니다.

집합 $T$에 $s$번 선분을 넣습니다. 그다음, 현재 집합 $T$에 있는 선분들 중 $s$바로 위에 있는 선분과 바로 아래에 있는 선분에 대해 선분 교차 판정을 한 후, 교차한다면 true를 리턴합니다.

 

8~11번 줄은 현재 event point가 선분의 오른쪽 끝점일 경우, 즉 $e = 1$인 경우입니다.

현재 집합 $T$에 있는 선분들 중 $s$바로 위에 있는 선분과 바로 아래에 있는 선분에 대해 선분 교차 판정을 한 후 교차한다면 true를 리턴합니다. 그다음, 집합 $T$에서 $s$번 선분을 제거합니다.

 

12번 줄에서는 스위핑이 끝났다면 false를 리턴합니다.

 

event point의 개수는 $2N$개이고, for문을 한 번 돌 때마다 $O(\log{N})$의 시간이 걸리므로 전체 시간복잡도는 $O(N\log{N})$임을 알 수 있습니다.

 

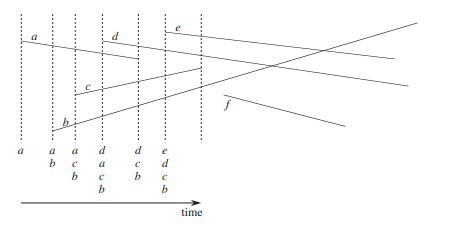
CLRS 1026p Figure 33.5

이해를 돕기 위해 예시를 가지고 직접 알고리즘을 수행해봅시다.

 

1번째 event point는 $a$의 왼쪽 끝점입니다. $a$를 $T$에 넣고, 위아래 선분과 교차 판정을 합니다. 위나 아래에 선분이 존재하지 않으므로, 다음 event point로 넘어갑니다.

 

2번째 event point는 $b$의 왼쪽 끝점입니다. $b$를 $T$에 넣고, 바로 위에 있는 선분인 $a$와 교차 판정을 합니다. 교차하지 않기 때문에 다음 event point로 넘어갑니다.

 

3번째 event point는 $c$의 왼쪽 끝점입니다. $c$를 $T$에 넣고, 바로 위에 있는 선분인 $a$, 바로 아래에 있는 선분인 $b$와 교차 판정을 합니다. 교차하지 않기 때문에 다음 event point로 넘어갑니다.

 

4번째 event point는 $d$의 왼쪽 끝점입니다. $d$를 $T$에 넣고, 바로 아래에 있는 선분인 $a$와 교차 판정을 합니다. 교차하지 않기 때문에 다음 event point로 넘어갑니다.

 

5번째 event point는 $a$의 오른쪽 끝점입니다. $a$의 바로 위 선분인 $d$와 바로 아래 선분인 $c$가 서로 교차하는지 확인합니다. 교차하지 않기 때문에 $a$를 $T$에서 제거하고 다음 event point로 넘어갑니다.

 

6번째 event point는 $e$의 왼쪽 끝점입니다. $e$를 $T$에 넣고, 바로 아래에 있는 선분인 $d$와 교차 판정을 합니다. 교차하지 않기 때문에 다음 event point로 넘어갑니다.

 

7번째 event point는 $c$의 오른쪽 끝점입니다. $c$의 바로 위 선분인 $d$와 바로 아래 선분인 $b$가 서로 교차하는지 확인합니다. 교차하기 때문에 1을 리턴합니다.

 

C++ 구현

위 알고리즘을 c++로 구현하면 다음과 같은 코드가 됩니다.

bool Any_Segments_Intersect(int n){
    vector<Event> S;
    multiset<Line> T;
    for (int i=0;i<n;i++){
        S.emplace_back(a[i].x1, 0, a[i].y1, i);
        S.emplace_back(a[i].x2, 1, a[i].y2, i);
    }
    sort(S.begin(), S.end());
    for (auto &P:S){
        CURX = P.x;
        if (!P.e){
            auto iter = T.insert(a[P.i]);
            if (next(iter)!=T.end()){
                if (intersect(*next(iter), a[P.i])) return 1;
            }
            if (iter!=T.begin()){
                if (intersect(*prev(iter), a[P.i])) return 1;
            }
        }
        else{
            auto iter = T.lower_bound(a[P.i]);
            if (iter!=T.begin() && next(iter)!=T.end()){
                if (intersect(*prev(iter), *next(iter))) return 1;
            }
            T.erase(T.lower_bound(a[P.i]));
        }
    }
    return 0;
}

또한, 위 구현에서 set의 비교조건을 sweep line $x=t$에서의 비교조건으로 해줘야 하기 때문에, 현재 sweep line의 $x$좌표를 저장하는 변수 CURX를 잡고, Line 구조체를 다음과 같이 만들었습니다.

ll CURX;
struct Line{
    ll x1, y1, x2, y2;
    Line(){}
    Line(ll _x1, ll _y1, ll _x2, ll _y2):x1(_x1), y1(_y1), x2(_x2), y2(_y2) {}
    bool operator<(const Line &L) const{
        long double tmp1 = (long double)(CURX-x1)/(x2-x1), tmp2 = (long double)(CURX-L.x1)/(L.x2-L.x1);
        return tmp1*(y2-y1) + y1 < tmp2*(L.y2-L.y1) + L.y1;
    }
};

비교조건은 선분과 sweep line의 교점의 $y$좌표를 직접 계산해서 비교했습니다. 실수를 사용하지 않고 +, -, * 연산만으로도 비교가 가능하지만 long long범위를 초과하기 때문에 사용하지 않았습니다.

 

정당성 증명

위 알고리즘이 1을 리턴한다면, 선분 교차 판정을 하면서 실제로 교차하는 선분 쌍을 찾았기 때문에 교점이 존재한다는 것을 알 수 있습니다. 따라서, 교점이 존재할 때, 반드시 1을 리턴한다는 것을 보이면 충분합니다.

 

교점 중 가장 $x$좌표가 작은(만약 여러 개면 $y$좌표가 가장 작은) 교점을 $P(p_x, p_y)$라고 합시다. 그리고 두 선분 $a$와 $b$가 교점 $P$에서 교차한다고 합시다. (가정에 의해 2개의 선분만 $P$를 지납니다.)

 

2개의 선분만 $P$를 지나고, sweep line이 $P$를 지나는 순간 크기 관계가 뒤바뀌기 때문에, 어떤 $q<=p_x$가 존재하여 $x=q$에서 $a$와 $b$가 집합 $T$에서 연속해있음을 알 수 있습니다.

 

그러면 가능한 시나리오는 2가지 밖에 없습니다.

1. $a$나 $b$가 집합 $T$에 추가되면서 $a$와 $b$가 연속하게 된다.

2. 처음에는 $a$와 $b$가 연속하지 않았지만 $T$에서 어떤 선분의 제거로 인해 연속하게 된다.

 

1번 케이스는 위에서 설명했던 의사코드의 4~7번째 줄이 감지하고, 2번 케이스는 8~11번째 줄이 감지합니다.

 

따라서, sweep line이 $P$에 도달하기 전 또는 도달한 시점에서 알고리즘이 1을 리턴한다는 것을 알 수 있습니다.

이 사실을 통해, 앞서 언급했던 set의 비교조건이 꼬이는 상황은 발생하지 않는다는 것 또한 알 수 있습니다.

 

 

만약 3개 이상의 선분이 한 점을 지나는 경우가 존재한다면 어떻게 해야 할까요? 이 경우에서도 적절한 선분 $a$와 $b$를 잡으면 $a$와 $b$가 모두 점 $P$를 지나면서, 어떤 $q<=p_x$가 존재하여 $x=q$에서 $T$에서 연속해있도록 할 수 있습니다. 따라서, 동일 논리가 적용 가능합니다.

 

이를 통해, $y$축에 평행한 직선이 존재하지 않는 모든 경우에 대해, 샤모스-호이 알고리즘이 올바르게 작동한다는 것을 알 수 있습니다.

 

일반적인 경우

지금까지 $y$축에 평행한 선분이 존재하지 않을 때에 대해서만 생각했습니다. 그렇다면 $y$축에 평행한 선분이 존재하는 경우에서는 어떻게 해결해야 할까요?

 

답은 의외로 간단합니다. 그냥 모든 선분에 대해 평행하지 않은 직선을 $y$축으로 설정하면 됩니다. 기존 좌표계에서는 $x=0$ 직선이 $y$축이였지만, $x+ky = 0$직선을 새로운 $y$축으로 설정해도 아무 문제가 없습니다. $x+ky = 0$직선을 새로운 $y$축으로 설정하게 되면, 기존 좌표계에서 $(x, y)$였던 점은 좌표가 $(x+ky, -kx+y)$로 변한다는 것을 알 수 있습니다. 따라서, 각 선분에 대해 기울기를 계산한 다음 적절한 $k$값을 설정해서 좌표계를 회전시키면 샤모스-호이 알고리즘을 적용시킬 수 있습니다.

 

위 방식을 사용할 경우 점의 좌표가 int범위를 벗어나기 때문에 점의 좌표를 long long으로 해주고, ccw 등을 할 때 __int128 자료형을 사용해줘야 합니다.

 

연습문제

https://www.acmicpc.net/problem/20150

20150번: 선분 교차 4

샤모스-호이 알고리즘의 구현 문제입니다. 그대로 구현하면 AC를 받을 수 있습니다.

 

https://www.acmicpc.net/problem/20151

20151번: 선분 교차 5

선분 교차 4와 거의 동일하지만 선분의 끝점끼리 만나는 것은 만나는 것으로 취급하지 않습니다.

선분 교차 판정만 약간 수정해주면 AC를 받을 수 있을까요? 아쉽게도 아닙니다.

 

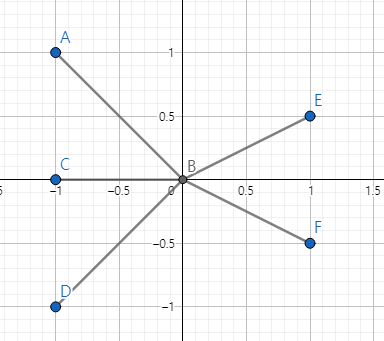
다음 그림과 같은 상황을 생각해봅시다.

선분 교차 판정만 수정한 상태로 샤모스-호이 알고리즘을 돌리게 되면, sweep line이 점 $B$에 있을 때, 집합 $T$에는 모든 선분이 들어가게 되고, 왼쪽 선분 3개를 제거해야 합니다. 하지만 현재 sweep line에서 모든 선분들의 $y$좌표가 같기 때문에, set에 원소를 넣거나 제거하는 연산이 정상적으로 작동하지 않습니다. 이 문제를 어떻게 해결해야 할까요?

 

풀이:

event point의 정렬 기준에서 $e$값을 내림차순으로 정렬합시다. 즉, $x$좌표가 같다면 제거를 먼저 하고, 그다음 추가를 합시다. 이렇게 해주면 선분 AB, CB, DB와 같이 오른쪽 끝점끼리 교차하거나 BE, BF와 같이 왼쪽 끝점끼리 교차하는 상황밖에 발생하지 않습니다.

 

오른쪽 끝점끼리 교차해서 $y$좌표가 같다면, sweep line의 $x$좌표를 1만큼 감소시킨 다음 비교하고, 다시 원래대로 되돌려 놓습니다.

왼쪽 끝점끼리 교차해서 $y$좌표가 같다면, 반대로 해주면 됩니다.

 

이렇게 해주면 비교조건이 제대로 작동하여 set이 정상적으로 작동한다는 것을 알 수 있습니다.

 

CLRS 33.2-4

Give an $O(n \log {n})$-time algorithm to determine whether an n-vertex polygon is simple.

 

풀이:

simple polygon은 다각형의 임의의 두 변이 서로 끝점에서만 교차하거나 교차하지 않는 다각형을 뜻합니다. 따라서, 선분 교차 5와 동일하게 풀 수 있습니다.

+특정 꼭짓점이 여러 번 나오지 않는다는 것도 체크해야 합니다.

 

참고: https://en.wikipedia.org/wiki/Simple_polygon

 

https://www.acmicpc.net/problem/9244

 

힌트:

샤모스-호이 알고리즘과 동일한 방식으로 스위핑을 하면서 set에 선분을 넣거나 뺄 때 인접한 위치에 있는 선분을 체크해봅시다.

 

https://www.acmicpc.net/problem/23244

https://www.acmicpc.net/problem/17155