Semi-local string comparison (수열과 쿼리 42)

 

길이가 각각 $N$, $M$인 두 문자열 $A$, $B$의 LCS (Longest Common Subsequence)을 구하는 문제는 매우 유명한 문자열 비교 문제이며, 이는 간단한 dp로 $O(NM)$에 해결할 수 있음이 알려져 있다. 또한, 이를 더 빠르게 하기 힘들다는 것도 알려져 있다. 이 글에서는 $A$와 $B$의 substring의 LCS를 구하는 문제인 semi-local LCS에 대한 빠른 알고리즘을 설명한다. 내용이 매우 길고 복잡하기 때문에, 이 글에서는 핵심적인 내용만 요약해서 설명할 것이며, 자세한 증명은 모두 생략할 것이다.

 

목차

1. ALCS algorithm

2. Seaweed braids

3. Unit-Monge matrix distance multiplication

4. Permutation string comparison

5. Extended seaweed matrix

 

1. ALCS algorithm

ALCS 문제는 임의의 $l, r$에 대해 $LCS(A, B[l, r])$를 빠르게 구하는 문제이다. 여기서 소개할 알고리즘은 전처리 시간복잡도 $O(NM)$, 공간복잡도 $O(N)$로 문제를 해결하기 위한 적절한 자료구조를 만들어내는 알고리즘이다. 문제 조건에 따라 다르지만 다음과 같은 시간복잡도에 문제를 해결할 수 있다.

 

1. 모든 $(l, r)$에 대해 계산: $O(N^2)$

2. $Q$개의 $(l, r)$에 대해 계산 (오프라인 쿼리): $O(N + Q\log N)$ ($Q \le N^2$이라 가정한다.)

3. $Q$개의 $(l, r)$에 대해 계산 (온라인 쿼리): $O((N+Q)\log N)$ (추가 메모리 $O(N\log N)$)

 

다음과 같은 격자 형태의 그래프를 생각하자.

 

1. 모든 점은 $x$좌표가 0이상 $N$ 이하, $y$좌표가 0 이상 $M$ 이하인 격자점이다.

2. $(x, y) \rightarrow (x, y+1)$ 간선과 $(x, y) \rightarrow (x+1, y)$ 간선이 항상 존재한다.

3. $(x, y) \rightarrow (x+1, y+1)$ 간선은 $A[x+1] = B[y+1]$일 때만 존재한다.

 

이를 두 문자열 $A$, $B$에 대한 GDAG라고 한다.

 

A = yxxyzyzx, B = yxxyzxyzxyxzx일 때 GDAG

 

모든 대각선 간선의 가중치를 1, 나머지 간선의 가중치를 0으로 놓자. 점 $(x, y)$에서 $(z, w)$로 가는 최장경로의 길이를 $C[(x, y), (z, w)]$라고 정의하자. 다음 식이 성립함을 쉽게 알 수 있다.

 

1. $C[(0, 0), (N, M)] = LCS(A, B)$

2. $C[(0, l), (N, r)] = LCS(A, B[l+1, r])$

 

이러한 그래프 모델링은 기존 문제와 완전히 동일한 형태의 문제면서 더 생각하기 편하다는 장점을 가지고 있기 때문에 앞으로 GDAG에서 최장경로를 구하는 문제에 대해 생각할 것이다.

 

GDAG에는 여러 다양한 성질들이 존재하지만 이 글에서는 핵심적인 성질 몇 개만 간단하게 짚고 넘어갈 것이다. 관심이 있다면 논문을 참고하거나, 직접 탐구해보는 것도 좋을 것이다.

 

1. 임의의 $i, j$에 대해, 어떤 $i_h(i, j)$가 존재하여,

$y < i_h(i, j)$이면 $C[(0, y), (i, j)] = C[(0, y), (i, j-1)]$

$y \ge i_h(i, j)$이면 $C[(0, y), (i, j)] = C[(0, y), (i, j-1)] + 1$

 

2. 임의의 $i, j$에 대해, 어떤 $i_v(i, j)$가 존재하여,

$y < i_v(i, j)$이면 $C[(0, y), (i, j)] = C[(0, y), (i-1, j)] + 1$

$y \ge i_v(i, j)$이면 $C[(0, y), (i, j)] = C[(0, y), (i-1, j)]$

 

위 성질들은 GDAG의 $C$값들에 대한 거의 모든 정보를 제공한다. ALCS 알고리즘은 $i_h$와 $i_v$를 dp를 이용해서 계산한 후, 이를 이용해서 LCS 쿼리를 처리한다.

 

다음 점화식이 성립한다.

 

$$i_h(0, j) = j$$

$$i_v(i, 0) = 0$$

$$i_h(i, j) = \begin{cases}
i_v(i, j-1) &(A[i] = B[j])\\
\max (i_v(i, j-1), i_h(i-1, j))&(A[i] \neq B[j])\\
\end{cases}$$

$$i_v(i, j) = \begin{cases}
i_h(i-1, j) &(A[i] = B[j])\\
\min (i_v(i, j-1), i_h(i-1, j))&(A[i] \neq B[j])\\
\end{cases}$$

 

위 점화식을 나이브하게 계산하면 공간복잡도와 시간복잡도 모두 $O(NM)$에 $i_v$와 $i_h$에 대한 모든 정보를 얻을 수 있다. 그러나 ALCS 문제에 직접적으로 필요한 정보는 $i_h$의 $N$번째 행뿐이다. 따라서, 간단한 토글링으로 $O(N)$의 메모리만 사용하면서 $i_h$의 $N$번째 행을 계산할 수 있다.

 

이제, $i_h$의 값을 이용해서 ALCS 문제를 해결하자. 식을 다음과 같이 변형할 수 있다.

$$C[(0, l), (N, r)] = C[(0, l), (N, l)] + cost(l, l+1) + \cdots + cost(l, r)$$

여기서 $cost(l, i) = C[(0, l), (N, i)] - C[(0, l), (N, i-1)]$이며, 이 값은 $l < i_h(N, i)$이면 0, 그렇지 않으면 1이라는 것을 $i_h$의 정의로부터 알 수 있다.

따라서, 위 식은 $i_h(N, [l+1, r])$에서 $l$보다 작거나 같은 수의 개수와 동일하고, 이는 2차원 상에서 직사각형 내의 점 개수를 세는 쿼리로 환원할 수 있다. 이는 PST / 쿼리정렬+세그+스위핑 등으로 해결할 수 있음이 잘 알려져 있다.

 

더 나아가, $i_h$의 모든 정보를 저장해두면 $LCS(A[1, i], B[l, r])$의 값도 빠르게 계산할 수 있다.

 

연습문제

Yosupo Judge: Prefix-Substring LCS

BOJ: LCS 9

IZhO 2013: Round words

Ptz Summer 2019 Day 8: Square Subsequences

 

2. Seaweed braids

ALCS 알고리즘은 매우 다양한 LCS 쿼리를 처리할 수 있지만, 전처리 시간복잡도가 기본적으로 $O(NM)$이 소요된다는 단점이 있다. LCS 자체가 $O(NM)$이 걸리는 문제이므로 일반적인 문자열에 대해 이보다 더 빠르게 할 수는 없지만, 순열과 같은 특수한 문자열에서는 제곱보다 빠르게 전처리를 하는 것이 가능하다. 2번과 3번 섹션에서는 이 알고리즘을 이해하기 위한 사전지식을 설명한다.

 

일단, ALCS의 작동과정을 다음과 같이 그림으로 표현할 수 있다.

$i$번째 열에서 시작한 선이 $j$번째 열에 도착했다면 $i_h(N, j) = i$라는 뜻이며, 왼쪽에서 출발한 선은 0의 값을 가진다. ($i_v(i, 0) = 0$이 전이되는 그림이다.)

이러한 형태로 선을 그리면 한 번 교차했던 선은 다시 교차하지 않는다는 특징을 가지게 된다. 이런 형태의 선의 집합을 seaweed braid라고 정의하고, 각각의 선을 seaweed라고 한다.

 

Def. seaweed braid는 다음 조건을 만족하는 선의 집합이다.

1. 윗쪽 가로선에는 seaweed의 시작점 $N$개가 존재하고, 아래쪽 가로선에는 seaweed의 끝점 $N$개가 존재한다. (모두 사용할 필요는 없다.)

2. 각 seaweed는 직선 형태이다. ( = 임의의 두 seaweed의 교점이 1개 이하이다.)

3. 어떤 두 seaweed도 시작점이나 끝점을 공유하지 않는다.

 

Def. 어떤 seaweed braid의 seaweed matrix는 다음과 같이 정의된다.

1. 모든 행과 열의 인덱스는 0 이상 $N$이하의 반정수

2. 시작점이 $i$, 끝점이 $j$인 seaweed가 존재하면 $P(i-\frac{1}{2}, j-\frac{1}{2}) = 1$

3. 나머지 값은 모두 0

정의에 의해 임의의 seaweed matrix는 각 행과 열에 1이 1개 이하로 있는 subpermutation matrix임을 알 수 있다.

 

Def. 2개의 seaweed braid에 대해 다음 그림과 같은 형태의 합성을 할 수 있다.

이 합성의 엄밀한 정의는 건너뛰겠다. 이러한 형태의 합성을 하면 두 개의 seaweed braid를 하나의 seaweed braid로 만들 수 있다는 사실만 알아두자. Seaweed braid는 이 연산에 대해 모노이드를 이룬다.

 

앞에서 봤던 ALCS 그림에서 왼쪽과 오른쪽 바깥으로 연결된 선들을 모두 지우면 $A$와 $B$에 대한 seaweed braid를 얻을 수 있다. 이 seaweed braid의 seaweed matrix를 생각해보면 이는 $i_h(N, j) = i$인 모든 $(i-\frac{1}{2}, j-\frac{1}{2})$에 1을 적은 행렬과 동일함을 알 수 있다. 또한, $A$의 각 문자와 $B$에 대해 seaweed braid를 만든 후 차례로 합성하면 $A$와 $B$에 대한 seaweed braid를 만들 수 있다. (행 단위로 각각 구한 후 합친다는 느낌으로 생각하면 된다.)

 

이를 식으로 적으면 다음과 같다.

$$P = P_1 \boxdot P_2 \boxdot \cdots \boxdot P_N$$

여기서 $P$는 $A$와 $B$에 대한 seaweed matrix, $P_i$는 $A[i]$와 $B$에 대한 seaweed matrix를 뜻하며, $\boxdot$은 두 개의 seaweed braid를 합성하는 연산과 동일한 연산이다.

 

3. Unit-Monge matrix distance multiplication

놀랍게도 두 seaweed braid를 합성하는 연산은 우리가 아는 연산의 조합으로 표현할 수 있고, 이를 $O(N\log N)$에 구하는 것 또한 가능하다.

 

편의를 위해 몇몇 기호를 정의하자. 앞으로 사용할 모든 인덱스들은 정수 혹은 반정수이고, 반정수의 경우 hat을 사용해서 표기한다. (ex. $\hat{i}$, $\hat{j}$)

• $[n_1:n_2]$는 $n_1$이상 $n_2$이하 정수의 집합을 뜻한다.
• $\langle n_1:n_2 \rangle$는 $n_1$이상 $n_2$이하 반정수의 집합을 뜻한다.
• 임의의 정수/반정수 $x$에 대해 $x^+ = x + \frac{1}{2}$, $x^- = x - \frac{1}{2}$이다.
• 두 집합 $I$, $J$에 대해 $(I | J)$는 $I$와 $J$의 데카르트 곱(Cartesian Product)이다.
• $\left [ i_0:i_1 | j_0:j_1 \right ] = \left ( \left [ i_0:i_1 \right ] | \left [ j_0:j_1 \right ] \right )$
• $\left \langle i_0:i_1 | j_0:j_1 \right \rangle = \left ( \left \langle i_0:i_1 \right \rangle | \left \langle j_0:j_1 \right \rangle \right )$

 

Def. $\left \langle 0:n | 0:n \right \rangle$에서 정의된 행렬 $D$에 대해, $D^{\Sigma}$는 $\left [ 0:n | 0:n \right ]$에서 정의되며 다음을 만족한다.

$$D^{\Sigma} (i, j) = \sum_{\hat{i} \in \left \langle i:n \right \rangle, \hat{j} \in \left \langle 0:j \right \rangle} D(\hat{i}, \hat{j})$$

즉, $D^{\Sigma}$는 $D$의 2차원 누적합 행렬이며, 왼쪽 아래에 있는 원소의 합을 나타낸다.

 

Def. $\left [ 0:n | 0:n \right ]$에서 정의된 행렬 $A$에 대해, $A^{\square}$는 $\left \langle 0:n | 0:n \right \rangle$에서 정의되며 다음을 만족한다.

$$A^{\square} (i, j) = A(\hat{i}^+, \hat{j}^-) - A (\hat{i}^-, \hat{j}^-) - A(\hat{i}^+, \hat{j}^+) + A(\hat{i}^-, \hat{j}^+)$$

 

이때, 임의의 $D$에 대해, $D = D^{\Sigma\square}$를 만족한다는 것을 알 수 있다. 이를 그림으로 나타내면 다음과 같다.

빨간색 행렬에 $\Sigma$를 취하면 검은색 행렬이 되고, 다시 $\square$를 취하면 원래 행렬로 돌아오는 것을 확인할 수 있다.

 

Def. $D$가 (sub)permutation matrix일 경우, $D^{\Sigma}$는 (sub)unit-monge matrix라고 한다.

 

Def. $\left [ 0:n_1 | 0:n_2 \right ]$에서 정의된 행렬 $A$와  $\left [ 0:n_2 | 0:n_3 \right ]$에서 정의된 행렬 $B$에 대해 행렬 $C = A \odot B$는 $\left [ 0:n_1 | 0:n_3 \right ]$에서 다음과 같이 정의된다.

$$C (i, k) = \min _ {j \in \left [ 0 : n_2 \right ]} \left ( A(i, j) + B(j, k) \right )$$

즉, $\odot$는 $(\min, +)$에서 정의된 행렬곱과 동일하며, 이는 distance multiplication이라는 이름으로 알려져 있다.

 

Thm. 두 subpermutation matrix $P_1$, $P_2$에 대해, 앞에서 정의했던 $\boxdot$ 연산은 다음과 같이 표현할 수 있다.

$$P_1 \boxdot P_2 = \left ( P_1 ^ {\Sigma} \odot P_2 ^ {\Sigma} \right ) ^ {\square}$$

즉, $\boxdot$ 연산은 두 (sub)unit-monge matrix에 대해 distance multiplication을 하는 연산과 동치이다.

 

Thm. $\left \langle 0:n | 0:n \right \rangle$에서 정의된 두 subpermuation matrix $P_A$, $P_B$에 대해 $P_C = P_A \boxdot P_B$를 $O(n \log n)$에 구할 수 있다.

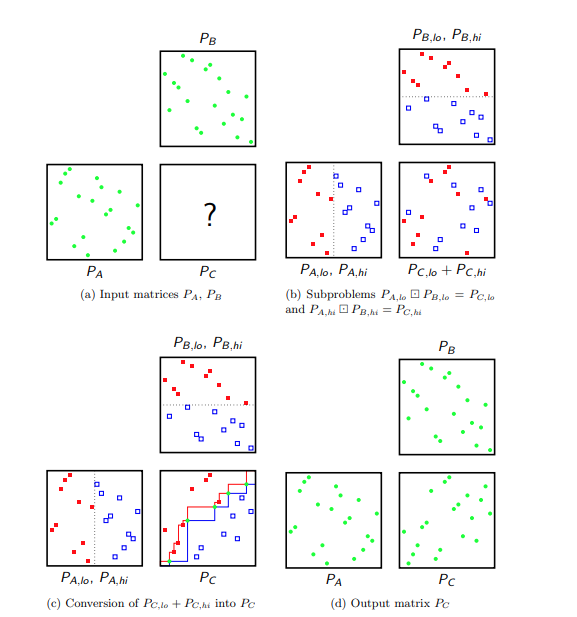
proof) 분할정복으로 문제를 해결한다. (두 행렬이 모두 permutation matrix일 때만 쓸 수 있는 방법이다. subpermutation matrix에 대한 방법은 후술.)

Recursion base: $n=1$일 때는 자명하다.

Recursive step: $n>1$일 때를 보자. 일반성을 잃지 않고 $n$은 짝수라고 하자. (홀수일 때도 동일한 방식으로 해결할 수 있다.)

 

Divide phase.

다음과 같이 $P_A$와 $P_B$를 절반으로 쪼개자.

$$P_A = \begin{bmatrix} P_{A, lo} & P_{A, hi} \end{bmatrix}$$

$$P_B = \begin{bmatrix} P_{B, lo} \\ P_{B, hi} \end{bmatrix}$$

$\boxdot$연산의 정의에 의해, $A$의 $i$번째 행이 모두 0이라면 $A \boxdot B$의 $i$번째 행도 모두 0이고, $B$의 $j$번째 열이 모두 0이라면 $A \boxdot B$의 $j$번째 열도 모두 0이다. 이를 이용하면 다음 행렬들을 재귀호출을 통해 계산할 수 있으며, 크기가 $\frac{n}{2}$인 부분문제 2개를 푸는 것과 동일하다.

$$P_{C, lo} = P_{A, lo} \boxdot P_{B, lo}$$
$$P_{C, hi} = P_{A, hi} \boxdot P_{B, hi}$$

$P_{C, lo}$와 $P_{C, hi}$는 모두 $\left \langle 0:n | 0:n \right \rangle$에서 정의된 행렬이라는 점에 유의하자.

 

Conquer phase.

여기서는 $P_{C, lo}$와 $P_{C, hi}$로부터 $P_C$를 복원한다. 다음과 같은 함수를 정의하자.

$$\delta(i, k) = \sum_{\hat{i} \in \left \langle 0:i \right \rangle, \hat{k} \in \left \langle 0:k \right \rangle} P_{C, hi}(\hat{i}, \hat{k}) - \sum_{\hat{i} \in \left \langle i:n \right \rangle, \hat{k} \in \left \langle k:n \right \rangle} P_{C, lo}(\hat{i}, \hat{k})$$

위 함수는 각 행과 열에 대해 단조증가한다는 점을 기억해두자.

 

$P_C(\hat{i}, \hat{k}) = 1$일 필요충분조건은 다음 3가지 조건 중 하나를 만족하는 것이다. (3가지 중 2개 이상이 동시에 성립하는 경우는 존재하지 않는다.)

$$\delta(\hat{i}^-, \hat{k}^-) < 0 \;  \textup{and}\; P_{C, lo}(\hat{i}, \hat{k}) = 1$$

$$\delta(\hat{i}^+, \hat{k}^+) > 0 \;  \textup{and}\; P_{C, hi}(\hat{i}, \hat{k}) = 1$$

$$\delta(\hat{i}^-, \hat{k}^-) < 0 \;  \textup{and}\; \delta(\hat{i}^+, \hat{k}^+) > 0$$

이 조건을 직접 확인하려면 너무 많은 시간이 소요되기 때문에 다른 판정법을 사용한다.

 

새로운 판정법은 $\delta$가 단조증가함수라는 점과 $\delta$의 부호만 중요하다는 점을 이용한다. $\delta$의 값이 음수에서 0으로 변하는 경계선, 0에서 양수로 변하는 경계선을 구한 후 이를 통해 조건을 판별하는 방식이다.

 

알고리즘 (음수에서 0으로 변하는 경계선을 구한다.):

1. $(\hat{i}, \hat{k}) = (n^+, 0^-)$에서 시작한다. 이때, $\delta(\hat{i}^-, \hat{k}^+) = 0$이다.

2. 현재 있는 위치에서 $\delta(\hat{i}^-, \hat{k}^+) < 0$일 경우, $(\hat{i}, \hat{k}+1)$로 이동한다. 그렇지 않을 경우, $(\hat{i}-1, \hat{k})$로 이동한다.

3. 새로운 위치에서 $\delta(\hat{i}^-, \hat{k}^+)$를 새로 계산한다. 이 값은 이전 위치에서의 $\delta$값과 $\delta$의 정의를 이용하면 $O(1)$에 구할 수 있다.

4. $\hat{i} = 0^-$ 또는 $\hat{k} = n^+$가 될 때까지 2, 3 과정을 반복한다. 그 이후 $(\hat{i}, \hat{k}) = (0^-, n^+)$까지 직선으로 이동하고 종료한다.

 

어떤 $d \in \left [ -n+1 : n-1 \right ]$에 대해, $\hat{k} - \hat{i} = d$를 만족하는 점 $(\hat{i}, \hat{k})$는 오른쪽 아래방향 대각선을 이루며, 방금 구했던 경계선과 유일한 교점 $(\hat{i}_{lo}, \hat{k}_{lo})$를 가진다. 이때, $r_{lo}(d) = \hat{i}_{lo} + \hat{k}_{lo}$로 정의한다. 비슷한 방식으로 0->양수 경계선을 구한 후, $r_{hi}(d)$를 동일하게 정의한다. 이를 모두 구했다면, 다음 조건을 만족할 때만 $P_C(\hat{i}, \hat{k}) = 1$라는 것을 알 수 있다.

$$\hat{i} + \hat{k} \le r_{lo}(\hat{k} - \hat{i}) \;  \textup{and}\; P_{C, lo}(\hat{i}, \hat{k}) = 1$$

$$\hat{i} + \hat{k} \ge r_{hi}(\hat{k} - \hat{i})\;  \textup{and}\;P_{C, hi}(\hat{i}, \hat{k}) = 1$$

$$\hat{i} + \hat{k} = r_{lo}(\hat{k} - \hat{i})\;  \textup{and}\; \hat{i} + \hat{k} = r_{hi}(\hat{k} - \hat{i})$$

첫 번째와 두 번째 조건은 $P_{C, lo}$와 $P_{C, hi}$의 1인 점들을 모두 확인하는 방식으로 $O(N)$에 확인할 수 있다. 세 번째 조건은 구했던 경계선을 스위핑하면서 확인하면 $O(N)$에 전부 확인할 수 있다.

 

따라서, Conquer phase를 $O(N)$에 처리했기 때문에 전체 시간복잡도는 $O(N \log N)$이 된다.

두 subpermutation matrix $P_A$, $P_B$에 대해 $P_A\boxdot P_B$를 계산하는 방법은 다음과 같다.

 

1. 1이 없는 $P_A$의 행과 $P_B$의 열을 모두 제거한다. 이 작업을 거친 후, $P_A$와 $P_B$는 각각 $n_1 \times n_2$, $n_2 \times n_3$ 크기의 행렬이 되며, $n_1 \le n_2$, $n_2 \ge n_3$가 성립한다.

2. $P_A$의 위쪽에 $n_2 - n_1$개의 행을 추가로 넣어서 크기가 $n_2$인 permuation matrix을 만든다.

3. $P_B$의 오른쪽에 $n_2 - n_3$개의 열을 추가로 넣어서 크기가 $n_2$인 permutation matrix을 만든다.

4. 이렇게 만든 두 permutation matrix에 대해 $\boxdot$을 계산하면 왼쪽 아래에 있는 $n_1 \times n_3$행렬이 $P_A \boxdot P_B$가 된다.

5. 과정 1에서 제거했던 행과 열을 복원해준다.

 

식으로 쓰면 다음과 같다.

$$\begin{bmatrix} * \\ P_A \end{bmatrix} \boxdot \begin{bmatrix} P_B & * \end{bmatrix} = \begin{bmatrix} * & * \\ P_C & * \end{bmatrix}$$

 

이 과정은 $O(N)$에 할 수 있기 때문에 시간복잡도는 여전히 $O(N \log N)$이다.

■

 

4. Permutation string comparison

지금까지 설명한 방식을 이용하면 $A$와 $B$의 seaweed matrix를 $O(NM\log N)$에 계산할 수 있다. 사실 ALCS를 돌리면 $O(NM)$에 구할 수 있기 때문에 일반적인 문자열에서는 별 의미가 없다. 그러나, $A$와 $B$가 모두 순열인 경우,  seaweed matrix를 $O(NM)$보다 빠르게 구하는 방법이 존재한다. 이를 이용하면 어떤 순열 $P$가 주어졌을 때, $P[l, r]$의 LIS(Longest Increasing Subsequence)를 쿼리당 $O(\log N)$에 처리하는 자료구조를 $O(N^2)$미만에 만들 수 있다.

 

Thm. 1이상 $N$이하의 원소로 구성된 길이가 $N$인 두 순열 $A$, $B$에 대해, $A$와 $B$의 seaweed matrix를 $O(N \log^2 N)$에 구할 수 있다.

proof) 분할정복으로 문제를 해결한다.

Recursion base: $n=1$일 때는 자명하다.

Recursive step: $n>1$일 때를 보자. 일반성을 잃지 않고 $n$은 짝수라고 하자. (홀수일 때도 동일한 방식으로 해결할 수 있다.)

 

Divide phase.

$A[1, \frac{n}{2}]$과 $B$, $A[\frac{n}{2} + 1, n]$과 $B$의 seaweed matrix를 각각 구한다. 이를 각각 $P_{lo}$, $P_{hi}$라고 하자. $A$와 $B$는 순열이므로, $P_{lo}(\hat{i}, \hat{i}) = 1$을 만족하는 $\hat{i}$가 정확히 $\frac{n}{2}$개 존재하며, $P_{hi}$도 마찬가지다. 이 점들을 미리 찾아두면 크기가 $\frac{n}{2}$인 부분문제 2개를 해결하는 것과 동일해지고, 이는 재귀호출로 처리할 수 있다. 시간복잡도는 $O(N)$이다.

 

Conquer phase.

$P = P_{lo} \boxdot P_{hi}$이므로 이를 구해주면 된다. 시간복잡도는 $O(N \log N)$이다.

 

따라서, 전체 시간복잡도는 $O(N \log^2 N)$이 된다.

■

 

5. Extended seaweed matrix

논문에서는 좀 더 다양한 형태의 LCS 쿼리를 지원하는 seaweed matrix에 대해 다룬다. 문자열 $B$의 앞뒤에 와일드카드(모든 문자와 매칭 되는 문자) $N$개를 추가로 붙이자. 즉, 문자열 $A$와 $?^NB?^N$의 ALCS를 생각해보자. 이를 그림으로 나타내면 다음과 같다. (그림에서는 n과 m이 반대로 되어있다.)

필요한 부분만 남기면 (a), (b)와 같은 형태가 되고, 이를 $\left \langle -N:M | 0:N+M \right \rangle$에서 정의한 seaweed matrix로 생각하면 이는 항상 permutation matrix이다. 또한, dnc를 할 때 (a)처럼 필요 없는 대각선(점선)을 따로 처리해주면 앞에서 설명했던 dnc를 그대로 적용해서 구하는 것이 가능해진다. 이를 $A$와 $B$의 extended seaweed matrix라고 하자. (논문에서는 이를 seaweed matrix라고 부른다.)

 

Def. $A$와 $B$의 extended seaweed matrix $P$에 대해, semi-local score matrix $H$는 $\left [ -N:M | 0:N+M \right ]$에서 다음과 같이 정의된다.

$$H(i, j) = j - i - P^{\Sigma}(i, j)$$

 

Thm. 다음 식들이 성립한다.

$$LCS(A, B[l+1, r]) = H(l, r)$$

$$LCS(A[l+1, N], B[1, r]) = H(-l, r) - l$$

$$LCS(A[1, r], B[l+1, M]) = H(l, N+M-r) - N + r$$

$$LCS(A[l+1, r], B) = H(-l, N+M-r) - N - l + r$$

 

증명은 생략한다.

 

연습문제

LOJ: 单位蒙日矩阵乘法 ($\boxdot$을 구현하는 문제다.)

BOJ: 수열과 쿼리 42

BOJ: 싱싱미역

 

참고문헌

[1] Alves, C. E. R., Cáceres, E. N., & Song, S. W. (2008). An all-substrings common subsequence algorithm. Discrete Applied Mathematics, 156(7), 1025-1035.

[2] Tiskin, A. (2008). Semi-local string comparison: Algorithmic techniques and applications. Mathematics in Computer Science, 1(4), 571-603.

[3] Tiskin, A. (2015). Fast distance multiplication of unit-Monge matrices. Algorithmica, 71(4), 859-888.